債券の残存期間を気にしたことはありますか?
債券は残存期間が長いほど、値動きが激しくなります。これを理論的に説明したのが「デュレーション」。残存期間が長い債券ほど、デュレーションが長くなり、値動きが激しくなります。
投資の世界で値動きの激しさは、リスクと同じ意味です。つまり残存期間が長い債券ほど、ハイリスクであり、その分ハイリターンを期待できるということです。
この記事では、デュレーションの概念を、計算方法とともに解説しています。巷の記事は、簡素すぎて要領を得ないか、計算式ばかりで難しすぎるかのどちらかの印象。というわけで、なるべく丁度いいレベル感にしてみました。
株式投資と組み合わせたときに、リスクを抑えて、最大限のリターンを狙う債券の選び方も解説しています。
債券投資の際に、格付けを気にする人は多いと思いますが、デュレーションも同じくらい大事な要素になってきます。債券投資に興味がある人は、ぜひ持って帰ってくださいね。
なお「債券の基本的な用語」や「利率と利回りの違い」「債券価格と金利の関係」が、いまいちピンと来ない人は、債券の基礎を解説した記事をサッと目を通してもらうと理解が捗ると思います。

債券のデュレーションとは?


デュレーション(Duration)は、「持続期間」や「継続期間」という意味の英単語です。
デュレーションは、債券投資における重要キーワード。投資の文脈でデュレーションと言われたときは、次のどちらかの意味です。
デュレーションの2つの意味
- 元本の平均回収期間
- 金利変動による債券価格の変動率
個人投資家が気にするのは、主に②でしょう。金利の変化によって、債券価格がどれほど大きく値動きするかです。
先に結論を言ってしまうと、
- 残存期間が長いほどデュレーションが長い(値動きが激しい)
- 利率が高いほどデュレーションが短い(値動きが緩やか)
となります。最終的にはこれだけ分かっていればOKかなと思います。
ただ、こういった指標を使うときは、どういうロジックでそうなるのかを理解することが大切です。なぜそうなるのか頭で分かっていないと、リスクを正確に把握できないからです。
①②の両者は、全く別のことを言っているようで、実はほとんど同じことを言っています。計算式もほとんど同じなので、一緒に見ていった方が理解が捗ります。
①「元本の平均回収期間」としてのデュレーション
第一のデュレーションの概念を噛み砕いて表現するなら、「債券を購入したときに払った金額が、何年後に回収できるか?」です。
デュレーション発案者の名に因んで、「マコーレー・デュレーション(Macaulay Duration)」と呼ばれています。
デュレーションが「3年」なら、投資資金を回収するのに3年かかるという意味です。デュレーションは「期間」を表す英単語なので、本来の意味からするとこちらがマッチします。
計算方法は次の通り。(式をわかりやすくするために、残存年数は3年としています)


まずは分母の「債券の現在価値」を見ていきましょう。これは現在の債券価格を計算する方法そのものです。


この計算が何をしているかと言うと、「将来」貰えるキャッシュフロー(毎年の利子と償還金額)を、「現在」の価値に割り引いています。
もっと噛み砕きましょう。金利2%の世界では、現在の100円は1年後に102円になっています。
そうすると1年後の100円は、現在の価値に直すと、100÷(1+0.02)=約98円になります。2年後の100円なら、現在価値は100÷(1+0.02)^2=約96.1円です。
そして、毎年のキャッシュフローを現在価値にして、全て足し合わせたものが、その債券の現在価値になります。
これが理論上の債券価格となります。
次は分子の方です。よく見ると、先ほど計算した債券の現在価値とよく似ていますね。


違うのは、毎年のキャッシュフローに、年数分の掛け算がされているところだけです。
結局のところ、デュレーション計算式が表しているのは、「毎年もらうキャッシュフローの現在価値の大きさを考慮した、元本を回収できるまでの年数」ということになります。
3年で償還を迎える債券が2つあったとします。
- 債券A:利率1%
- 債券B:利率10%
どちらの債券も、投資元本を回収できるのは3年後ですね。利率がちょっとやそっと高かろうと、大部分の金額が返ってくる3年後にならないと全額回収はできません。
このとき、両者の元本回収期間を、同じ3年と評価して良いのでしょうか?
全額回収はできないとしても、利率10%の債券Bの方が、早めに投資元本の一部を回収しています。両者の元本回収期間を、同じ3年とするのは不公平でしょう。
「償還前に回収できる投資元本の一部も、きちんと評価してあげましょう」というのが、デュレーションの計算式が意図していることです。
実際にデュレーションを計算してみよう
次の3つの債券のデュレーション(元本の平均回収期間)を求めてみました。
金利(利回り)は2%と仮定しています。
| 債券A | 債券B | 債券C | |
| 額面金額 | 100円 | 100円 | 100円 |
| 利子 | 5円 | 10円 | 5円 |
| 残存期間 | 5年 | 5年 | 10年 |
| デュレーション | 4.58 | 4.30 | 8.35 |
【債券A】を基準にして、
- 利率が高い【債券B】
- 残存期間が長い【債券C】
のデュレーションがどう変化しているか注目しましょう。
デュレーションの法則の通り、
- 利率が高いほどデュレーションが短い
- 残存期間が長いほどデュレーションが長い
と確認できましたね。
利率が高い【債券B】は、早く資金を回収できるので、デュレーションは短くなっています。
償還が10年先と遠い【債券C】は、大部分の投資元本が帰ってくるのが遅いため、資金回収に時間がかかります。そのためデュレーションが長くなっています。
債券の利率はたかが知れているので、デュレーションに大きな違いは出ませんが、残存期間の長さは大きな違いを生みます。
②「金利変動による債券価格の変動率」としてのデュレーション
もう一つのデュレーションの概念は、「金利が変化したときに、どれだけ債券価格が変化するかを数値化したもの」です。
こちらは「修正デュレーション(Modified Duration)」と呼ばれる概念です。デュレーションが長いほど、金利に反応して大きく値動きします。
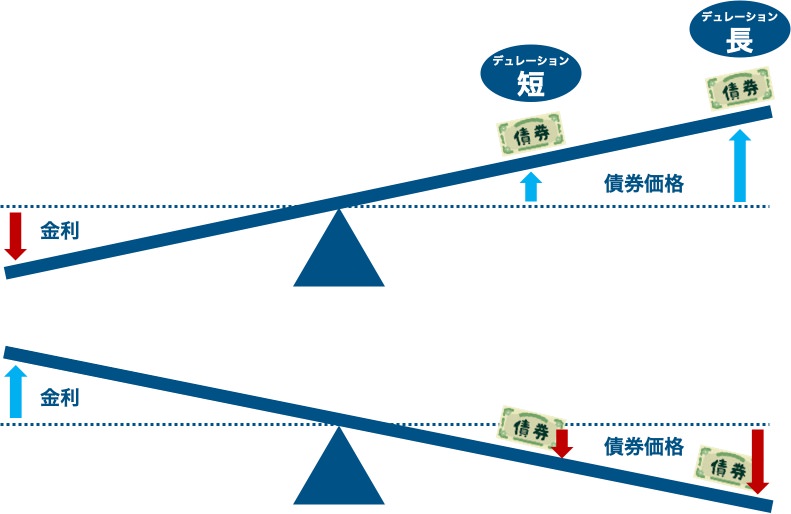

- 修正デュレーションが「1」なら、
金利が1%上昇したときに、債券価格は1%下落します。
- 修正デュレーションが「3」なら、
金利が1%上昇したときに、債券価格は3%下落します。
*金利と債券価格は逆に動きます
修正デュレーションの計算方法は、上記の「マコーレー・デュレーション」を最終利回りで割っただけ。


そのため実際には、「マコーレー・デュレーション」を、そのまま金利と債券価格の感応度として使ってもほとんど差し支えありません。
先程の3つの債券で、修正デュレーションを計算すると次のようになります。
| 債券A | 債券B | 債券C | |
| 額面金額 | 100円 | 100円 | 100円 |
| 利子 | 5円 | 10円 | 5円 |
| 残存期間 | 5年 | 5年 | 10年 |
| マコーレー・デュレーション(元本の平均回収期間) | 4.58 | 4.30 | 8.35 |
| 修正デュレーション(金利変動による価格感応度) | 4.49 | 4.22 | 8.18 |
残存期間の長さが強く影響しているのがわかると思いますね。そのため、残存期間が長い債券ほど、値動きが激しくなる傾向があります。
国債のデュレーション別チャート&リターンを比較

デュレーションの概念は、概ね説明しきれたと思います。ここからはデュレーションの違いが、チャートや利回りにどう跳ねてくるのかを見ていきましょう。
今回は次の3種類のETFで、チャートやリターンを分析してみたいと思います。いずれも業界大手のブラックロック社が運用している、米国債を対象としたETFです。
| SHY(短期) | IEF(中長期) | TLT(超長期) | |
| 投資対象 | 1-3年の米国債 | 7-10年の米国債 | 20年超の米国債 |
| 平均残存期間 | 1.97年 | 8.47年 | 26.4年 |
| 実効デュレーション | 1.95年 | 7.89年 | 18.82年 |
*実効デュレーションは、もう少し複雑な概念ですが、ここでは気にしなくて大丈夫です。
まずチャートから見てみましょう。
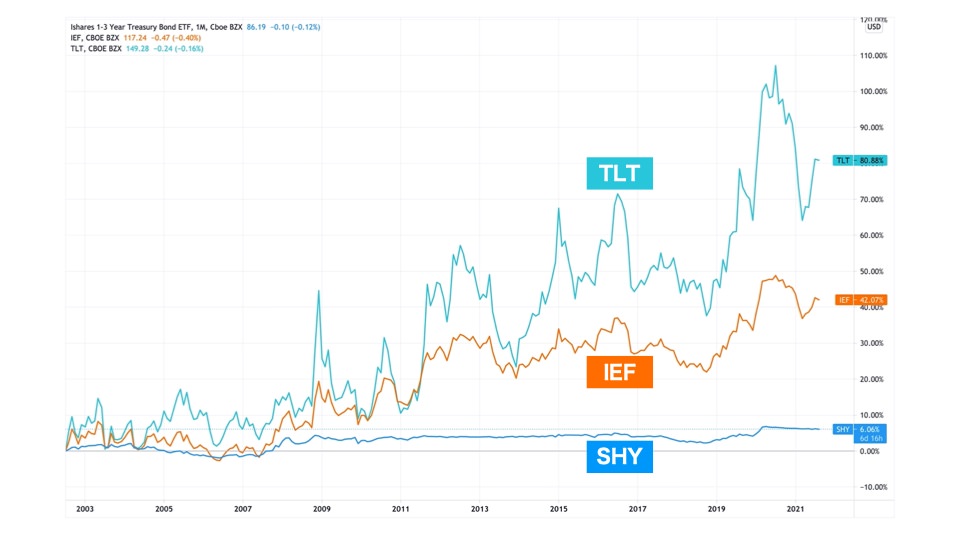

デュレーションが長い「TLT(超長期国債)」の値動きが激しくなっています。この3者で比べると、デュレーションが最も短い「SHY(短期国債)」はほぼ水平に見えますね。
法則通り、デュレーションが長いほど、値動きが激しいことが確認できました。
もう一つ気づくのは、値動きが激しいほど、値上がり幅も大きいということ。「TLT(超長期国債)」は、キャピタルゲイン(値上がり益)も期待できそうです。
続いて利回り(ここでは、配当+値上がり益の総合リターンを指している)も見ていきましょう。
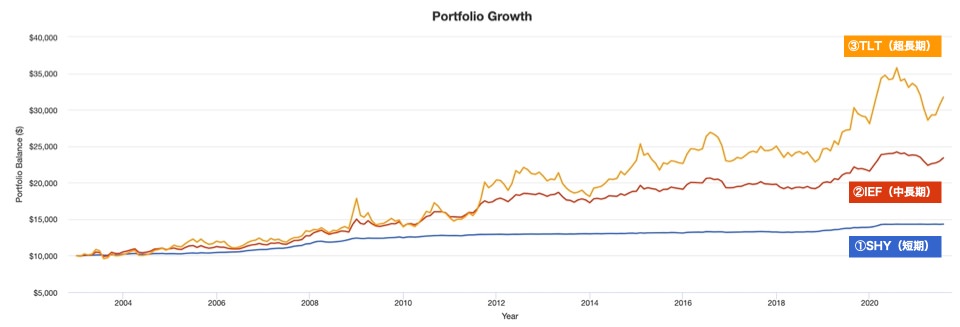

| SHY(短期) | IEF(中長期) | TLT(超長期) | |
| 年平均成長率 | 1.95% | 4.68% | 6.41% |
| 標準偏差 | 1.29% | 6.26% | 13.10% |
| 最も伸びた年 | 7.35% | 17.91% | 33.96% |
| 最も落ち込んだ年 | 0.02% | -6.59% | -21.80% |
| 最大下落幅 | -1.18% | -7.60% | -21.80% |
| シャープレシオ | 0.61 | 0.57 | 0.45 |
*青字は三者の中でパフォーマンスが最も良い。赤字はパフォーマンスが最も悪い。
利回りもデュレーションが長い順に大きくなっていますね。その代わり、マイナスになる幅も大きくなっています。
デュレーションの長さは、そのままリスク・リターンの大きさと言えますね。
なお債券の残存期間と利回りの関係は、「イールドカーブ」が有名です。イールドカーブの解説記事で、利回りが上下する要因を詳しく解説しています。
ちなみにイールドカーブの曲線の傾きは、景気の先行きを占う重要な経済指標となっています。こちらも知っておくと、金融リテラシーが上がります。


株式と組み合わせたポートフォリオに最適なデュレーションは?


個人投資家であれば、株式をメインで保有しつつ、暴落時に資産を守る役割として、債券を組み入れるケースが多いと思います。このケースを前提に考えてみましょう。
メインの投資先は、米国の代表的な株価指数である「S&P500」と仮定します。米国株中心のインデックス投資をしている人は、ドンピシャで当てはまります。
S&P500と組み合わせたときに、どのデュレーションの債券がもっとも資産を防衛しつつ、リターンを増やせるかを検証してみたいと思います。
まず、先程の「SHY(短期国債)」「IEF(中長期国債)」「TLT(超長期国債)」のチャートに、S&P500も加えてみましょう。
次のチャートは、2020年のコロナショックを切り取っています。
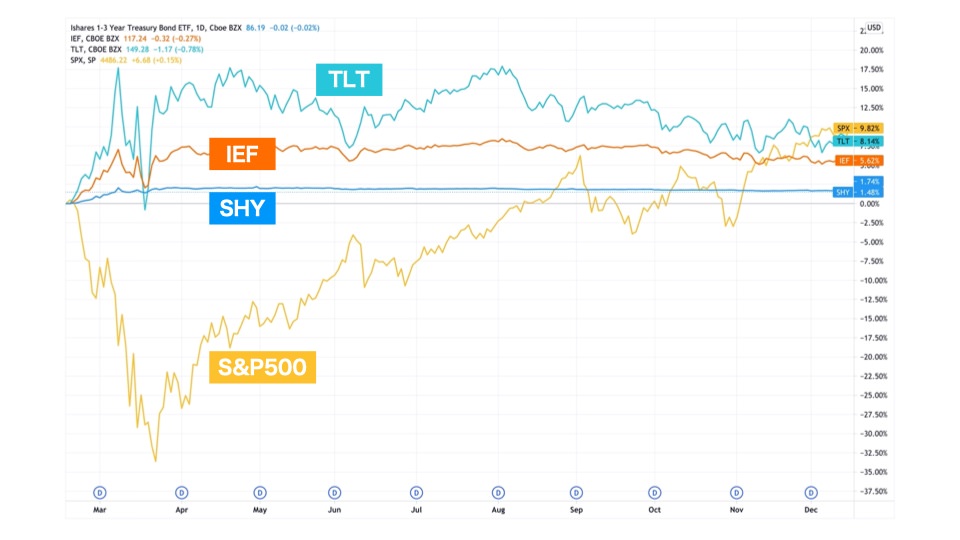

S&P500が最大-30%超も下落したのに対し、
- SHY(短期国債):チャートにほとんど動きがありません
- IEF(中長期国債):最大で8%ほど上昇しています
- TLT(超長期国債):最大18%上昇してしています
S&P500が回復するにつれて、徐々に値下がりしている傾向が見えます。
デュレーションが長い長期国債は、値動きが激しい分だけ、株価の下落を相殺するように値動きすることがわかります。
厳密には、長期国債は景気動向の影響を強く受けるので、金利とは別の要因で動いています。ただ結果として、値動きの激しさが、株式の損失を補うように機能しています。
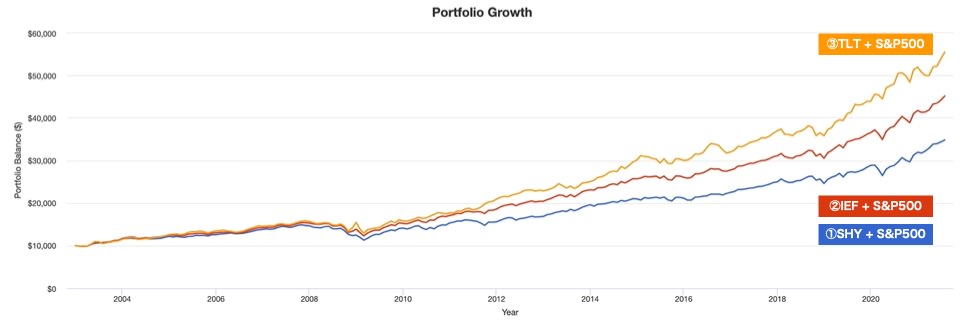
続いて、同じ組み合わせのトータルリターンを見てみましょう。チャートは値動きだけですが、こちらは配当も込みの総合リターンです。

| SHY+ S&P500 |
IEF+ S&P500 |
TLT+ S&P500 |
|
| 年平均成長率 | 6.94% | 8.45% | 9.66% |
| 標準偏差 | 6.74% | 6.68% | 8.12% |
| 最も伸びた年 | 17.30% | 19.63% | 22.67% |
| 最も落ち込んだ年 | -15.09% | -9.45% | -3.08% |
| 最大下落幅 | -24.19% | -20.14% | -18.17% |
| シャープレシオ | 0.85 | 1.06 | 1.03 |
*S&P500はSPYを使用。債券と株式の割合は50:50とする。
*青字は三者の中でパフォーマンスが最も良い。赤字はパフォーマンスが最も悪い。
デュレーションが長い「TLT(超長期国債)」のリターンが大きいのは、当然の結果でしょう。
ただ、下落局面の底堅さでも、「TLT(超長期国債)」と組み合わせたポートフォリオが一番でした。リーマンショックの年でも、わずか-3%の傷で済んでいます。
この現象が起きる理由は、デュレーションが長い債券の方が値動きが激しいので、株式の値下がり分をカバーしやすくなっているからです。
投資の世界においては、「値動きの激しさ=リスク」です。単体ではリスクの高い長期国債ですが、株式と組み合わせたときは最もリスクが小さくなるのです。
ちなみに債券はその性質上、一発当てて大儲けというシナリオが存在しないので、個別銘柄に投資する意味がほとんどありません。分散投資できるETFが最適です。
米国の債券ETFを選ぶ際は、「債券はETF一択!定番の米国債券ETFを一挙紹介」も参考にしてみてください。























